感知机及Python简单实现

1. 感知机简介

感知机是最简单的神经网络（单层神经网络），由它可以组成复杂的多层神经网络（Multilayer Perceptron），是学习复杂神经网络的基础。1957年，由Frank Rosenblatt首先提出，模仿人类的神经元工作原理，实现了线性二元分类的目的。神经元是由突触，树突，轴突和细胞体组成。突触是在神经元轴突的末端，在突触前端还有突触小泡，可以释放神经递质，作用于另一神经元的树突前端，在突触这个部位就完成了神经信号的传导。对于神经元来说，树突可以电信号的方向输入刺激，而细胞体就负责接收这些电位信息后决定是否向轴突发出电信号，所以轴突是神经元的输出端。
而感知机模仿了神经元的输入，处理和输出部分，一个简单的感知机结构如下图

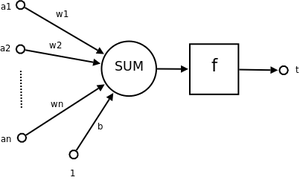
图中$a_n$是输入变量，每个输入变量有对应的权重$w_n$，最近求得输入的总和$\sum_{i}^{n}{a_i w_i}$，当感知神经元接收到输入后，需要判断是否发出信号，这里就需要变量$b$作为阈值，大于等于$b$时就发出信号，小于$b$时就不发出信号，整理成下面的条件方程：

$$ y = \begin{cases} 1, & \text{$\sum_{i}^{n}{a_i w_i} \geq b$} \\ 0, & \text{$\sum_{i}^{n}{a_i w_i} < b$} \end{cases} $$

如果把多个输入变量和对应的权重放到向量$x$和$w$中，两个向量的点积$x \cdot w$就是等于$\sum_{i}^{n}{a_i w_i}$，同时将$b$从不等式的右边调到左边，变成下面的形式

$$ y = \begin{cases} 1, & \text{$w \cdot x + b \geq 0$} \\[2ex] 0, & \text{$w \cdot x + b < 0$} \end{cases} $$
可以看出，最后需要关注的是方程 $w \cdot x + b$，$w$ 为权重项，$b$为偏置项。如果能够获得这两个参数，那么感知机也就确定下来了。

2. 学习策略

假设有一个数据集是线性可分的，那么会存在一个超平面区分正负样本，在超平面之上的为正样本，超平面之下的为负样本。如果超平面为$x \cdot w + b$，那样本可以用

$$ y = \begin{cases} 1, & \text{$x \cdot w + b \geq 0$，正例} \\[2ex] -1, & \text{$x \cdot w + b < 0$，负例} \end{cases} $$

如果确定了参数$w$和$b$，那就确定了平面，也就能对样本进行分类。为了能够找到合适的参数，对感知机确定一个损失函数，通过求解损失函数来获得想要的参数。损失函数可以统计误分类点到超平面的距离

$$ d = \frac{1}{||w||}|w \cdot x + b| $$ 如果一个点是误分类点，那么

$$ -y \cdot (w \cdot x + b ) > 0 $$

所有误分类点到超平面的距离可以表示为：

$$ d = - \frac{1}{||w||} y(x \cdot w + b) $$

这里的距离称为几何距离，几何距离因为添加了$||w||$分母，可以抵消参数$w$的变量对距离的影响。为了方便计算，可以把分母去掉，得到的是函数间隔，所有误分类点到超平面的距离之和为

$$ L(w,b) = - \sum y(x \cdot w + b) $$

下面就是如何找到一个合适参数让上面的函数最小 ，$\min_{a,b} L(w,b) = -\sum y(x \cdot w + b)$。这里使用随机梯度下降法来获取合适的参数，设定一个$w_0,b_0$，从误分类点中随机选择一个点，沿着该点梯度下降的方法，更新$w,b$，上面损失函数的梯度可以表示为

$$ \nabla_{w} L(w,b) = -\sum yx \\ \nabla_{b} L(w,b) = -\sum y $$

对于误分类点$(x_i,y_i)$，$w,b$更新过程如下：

$$ w \leftarrow w + \eta y_i x_i \\ b \leftarrow b + \eta y_i $$ $\eta(0 \leq \eta < 1)$指示梯度下降的程度，可以理解成模型从数据中学习程度的快慢。不断从为误分类的数据集中挑选数据，让参数$w,b$往损失函数减小的方向进行更新。根据导数的意义，导数是曲线的切线，是表示切点的变化率，往导数方向进行更新，比起漫无目的地更新，效果更好，能更快地达到极值点（或许只是局部的极值）。

权重和偏置两个参数，我们希望模型能从模型中学习。在学习初始时，先给权重和偏置一个初始值，比如为0，挑选其中一个样本，按照初始的权重和偏置计算，如果计算符合预期，那取另一个样本。当遇到结果不符样本时，就更新权重和偏置，再用新的权重和偏置对样本进行测试，直到所有样本都能有正确的分类。

3. 感知机的Python实现

在堆码之前，要确保使用的数据是线性可分的，不然算法会陷入死循环中

# 统计学习方法书中的几个测试点
def percepton(x,y):
    # 设置初始值
    w,b = (0,0), 0
    # 学习率设为1
    n=1

    i=0
    while True:
        if i+1 > len(x):
            break
        # 判断是不是误分类点
        out = y[i]*(w[0]*x[i][0] + w[1]*x[i][1]+b)

        if out <= 0:
            # 更新参数
            w = (w[0] + n*y[i]*x[i][0], w[1] + n*y[i]*x[i][1])
            b = b + n*y[i]
            print(i, 'w:',w,'b:', b)
            i = 0
        else:
            i+= 1
    return w,b   

x= [(3,3), (4,3), (1,1)]
y = [1,1,-1]
percepton(x,y)

输出误分类点处参数的变化

0 w: (3, 3) b: 1
2 w: (2, 2) b: 0
2 w: (1, 1) b: -1
2 w: (0, 0) b: -2
0 w: (3, 3) b: -1
2 w: (2, 2) b: -2
2 w: (1, 1) b: -3

在三维里画了样本点和区分的超平面，从2维的点扩展到了三维，超平面看起来有点分不清方向，可以换个交互式的看看结果。上面的代码按照随机梯度下降的方法实现了一个简单的感知机。

4. 感知机的对偶形式

感知机的对偶形式¹将$w$和$b$用$x$和$y$的线性组合来表示。$w$和$b$的初始值为0，误分类点$(x_i,y_i)$更新参数

$$ w \leftarrow w + \eta x_i y_i \\ b \leftarrow b + \eta y_i $$ 感知机在学习的过程中，对该误分类点一共利用了$n$次，每次都用参数进行了调整，那最终以该来计算参数变化：

$$ \Delta w_i = \sum_{j=1}^{n}n_j \eta x_i y_i \\ \Delta b_i = \sum_{j=1}^{n}n_j \eta y_i $$ 用$a_i$来表示该点的更新总量$a_i = \sum_{j=1}^{n}n_j \eta$，那经过所有点的学习后，参数$w$和$b$表示为

$$ w = \sum_{i=1}^{N} a_i x_i y_i \\ b = \sum_{i=1}^{N} a_i y_i $$ 这里$N$表示所以的样本总数，也包括了正确分类的点。因为对于正确分类的点来看，感知机在学习的时候是使用了0次，对应$n$为0。那最前面用来判断点是否被误分类的公式就可以改成

$$ y_i(\underbrace{\sum_{j=1}^{N}a_j y_j x_j}_{w} x_i) + b \leq 0 $$

需要注意下$i$和$j$小标，$i$是区分需要误差的点，$j$是计算更新总量时用到的点。为了便于区分，特意添加了括号以指标变换前的参数。每次更新时的参数就变成了

$$ a \leftarrow a + \eta \\ b \leftarrow b + \eta y_i $$ 经过变换后，判别误分类的公式里面出现了向量的内积组成的Gram矩阵$[x_j\cdot x_i]$，该矩阵的出现有一个好处就是我们可以提前把内积计算好，等用的时候就可以直接提取了，向量$(3,3), (4,3), (1,1)$的Gram矩阵$G$如下：

$$ \begin{bmatrix} 18 & 21 & 6 \\ 21 & 25 & 7 \\ 6 & 7 & 2 \\ \end{bmatrix} $$

可以看出$G_{ij} = x_i \cdot x_j$，Gram矩阵维度是$N \times N$，其中$N$表示样本的数量，如果数据中变量很多，比样本量大的多的话，就会体现出计算优势。因为前面随机梯度下降的计算是消耗在$w \cdot x$内积的计算的，这个是和特征变量成正比，而前面的Gram矩阵是和样本数成正比的，因此如果特征变量数目大于样本数的话，对偶形式可以更加快速地完成计算。

def perceptonGram(x,y):
    # 设置初始值
    a = np.zeros(x.shape[0])
    b = 0
    # 学习率设为1
    n=1

    i=0  # 从第一个变量开始循环监测
    wrong_i = -1    # 误分类点的索引
    gramM = x.dot(x.T)
    while True:
        if i+1 > len(x):
            break
        # 判断是不是误分类点
        out = y[i]*(np.dot(np.multiply(a, y), gramM[:][i]) + b)

        if out <= 0:
            # 更新参数
            a[i] = a[i] + n
            b = b + n*y[i]
            print("x%s" % (i+1), 'a:',a,'b:', b)
            wrong_i = i

        elif out > 0 and wrong_i == i:
            i = 0 
            wrong_i = -1
        else:
            i+= 1
    return a,b   

x = np.asarray(x)
y = np.asarray(y)
perceptonGram(x, y)

变量更新过程

x1 a: [1. 0. 0.] b: 1
x3 a: [1. 0. 1.] b: 0
x3 a: [1. 0. 2.] b: -1
x3 a: [1. 0. 3.] b: -2
x1 a: [2. 0. 3.] b: -1
x3 a: [2. 0. 4.] b: -2
x3 a: [2. 0. 5.] b: -3

示例参考了《统计学习方法》中的点，更新的过程也与书中的结果一致。需要注意一下numpy.dot和numpy.multiply的使用方法，对于$x_1$来说，$\sum_{j=1}^{N}a_j y_j x_j x_i$，可以分解为下面几个公式之和

$$ a_1 y_1 x_1 x_1 \\ a_2 y_2 x_2 x_1 \\ a_3 y_3 x_3 x_1 $$ 其中$x_j x_i$部分是位于Gram矩阵的$i$列，具体计算过程可以参考代码。